Kategorie

English

Úvod

Zásady umístění antén na pozemních stanicích

Při rozboru různých konfigurací antén na pozemních stanicích bych ještě rád připomněl pojem Fresnelovy zóny, abyste nehledali chybu v anténním systému, zatímco je někde úplně jinde.

Pro přenosové frekvence, o kterých v FPV hovoříme, je nutnou podmínkou přímá viditelnost mezi vysílačem a přijímačem, ale to nestačí – volný musí zůstat i jistý prostor okolo této spojnice, tzv. Fresnelova zóna.

Pokud do této zóny vstupují jakékoli překážky, dochází ke zhoršení přenosu a při zakrytí více než cca 40% Fresnelovy zóny se již přenášený obraz rozpadá, přitom na vině není malý výkon vysílače nebo chybná anténní soustava přijímače! Totéž platí i pro přenos signálu z RC-soupravy, kde nadměrné zakrytí Fresnelovy zóny může vést ke ztrátě kontroly nad modelem.

Fresnelova zóna prvního řádu má tvar rotačního elipsoidu s krajními body v místě vysílače a přijímače, osa tohoto elipsoidu je totožná se spojnicí vysílače a přijímače.

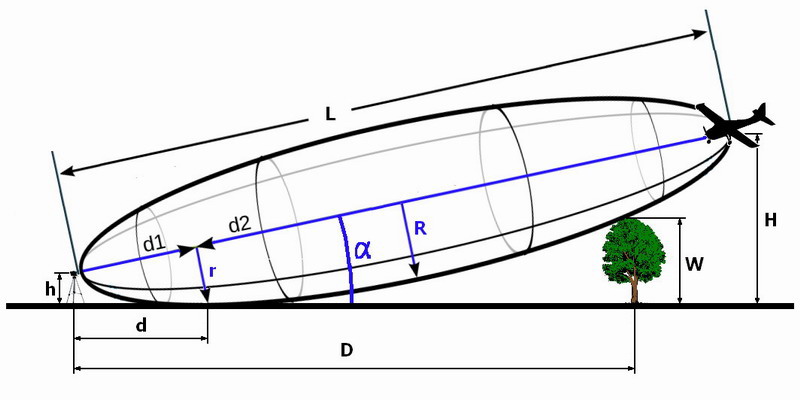
Při spojení na vzdálenost L poloměr Fresnelovy zóny r v libovolném místě spojnice vysílače a přijímače určíme ze vztahu

r = sqrt (λ*d₁*d₂/(d₁+d₂)) (m)

V této rovnici d₁ a d₂ jsou dílčí úseky spojnice v místě, kde určujeme poloměr Fresnelovy zóny, přičemž platí d₁ + d₂ = L

Vlnovou délku λ určíme ze vztahu

λ = c/f,

kde c je rychlost světla 300 000 000 m/s, f je přenosová frekvence v Hz.

Největšího poloměru R dosahuje Fresnelova zóna v polovině spojnice mezi vysílačem a přijímačem. Dosazením za d₁ = d₂ = L/2 získáme

R = ½*sqrt (λ*L) (m)

Následující tabulka uvádí maximální poloměr Fresnelovy zóny pro různé frekvence a spojovací vzdálenosti:

Stojí-li přijímačová anténa pro vlnovou délku λ na stativu ve výšce h, pak při spojení na vzdálenost větší než

L_min = 4*h²/ λ (m)

bude mít Fresnelova zóna poloměr větší než je výška antény nad zemí.

Pro frekvenci 5.8GHz vychází Fresnelova zóna o nejmenším poloměru. Při výšce antény 150cm nad zemí se jedná o spojení na 174 metrů, ale video přenos budeme určitě chtít provozovat na vzdálenost větší.

Pro spojení na vzdálenost L > L_min je nutné anténu zvednout nad horizont nejméně pod úhlem α, přičemž tento úhel se se spojovou vzdáleností několikrát větší než L_min již prakticky nemění.

cos α ≈ sqrt (4*h² / (λ²+4*h²))

α ≈ arccos (sqrt (4*h² / (λ²+4*h²)))

Tento minimální úhel pro různé výšky antény nad zemí a pro časté FPV frekvence je uveden v následující tabulce:

Fresnelova zóna se dotkne povrchu země ve vzdálenosti d od pozemní stanice

d ≈ λ /2 * (cos α / (1- cos² α))

Současně ve vzdálenosti D by se neměla vyskytovat žádná překážka vyšší než W

W ≈ D * tan α – sqrt ((λD/cos α)*(L- (D/cos α))/L)

protože jinak tato překážka naruší Fresnelovu zónu.

Fresnelova zóna může být narušena i částečně propustnými překážkami, jako např. mraky nebo neolistěnými stromy (ty olistěné zvláště pro pásmo 5.8GHz představují takřka nepropustnou překážku). Při umístění pozemní stanice na hřebenu kopce může být anténní systém orientován vodorovně nebo sklopen i dolů, ale pak zas nesmíme zapomínat na okolní hřebeny a vrcholy, které mohou do Fresnelovy zóny vstupovat.

Nezapomínejme ani na řídící signál RC-soupravy, pro nějž zásady Fresnelovy zóny platí také, přičemž její poloměr je v případě řídící frekvence 2.4GHz ještě větší než pro 5.8GHz zpravidla používaných pro video přenos. Pokud používáme anténu integrovanou na RC-soupravě, nachází se cca 1m nad zemí, Fresnelova zóna se pak počíná narušovat vodorovným povrchem již při klesnutí modelu méně než cca 7° nad horizont!

Z uvedených faktů vyplývají tato poučení:

• Fresnelova zóna se díky eliptickému tvaru zpočátku velmi rychle rozšiřuje. Při spojení na 700m a frekvenci 2.4GHz je její maximální průměr 9.4m, ale již 10m před anténou má průměr 1.1m. Jsou-li antény sklopeny nízko nad horizont, v prostoru před nimi by se neměly nacházet jakékoli překážky nebo zdržovat osoby, a to ani ve vzdálenosti desítek metrů, kde se Fresnelova zóna ještě stále nachází v těsné blízkosti povrchu.
• Antény umísťujeme v rovném terénu na stativ co nejvýše, zvláště předpokládáme-li let modelu nízko nad horizontem.
• Není rozumné pouštět se v rovinném terénu při běžné výšce stativu 1,5m s modelem méně než 3° nad horizont.
• Čím nižší frekvence, tím výše na stativ je nutné antény umístit. Právě pásma 433MHz a 900MHz jsou vhodná pro dálkové rekordy v FPV, avšak velikost Fresnelovy zóny by vyžadovala umístění anténního systému na nepřiměřené vysokou konstrukci. Proto se při takových pokusech umísťuje pozemní stanice na hřeben kopce, kde anténní systém může vyzařovat takřka vodorovně do prostoru a dosáhnout tak nízkých poloh modelu nad horizontem.

K odhadu výšky modelu nad horizontem je výhodné využít porovnání s představou měsíce či slunce na daném místě horizontu. Jejich úhlový průměr je přibližně půl stupně.

Zpět